-
La Règle de l'Hospital
La Règle de l'Hospital
La Règle de l'Hospital : en 3 étapes
Soit f(x) = g(x) / h(x) et nous voulons calculer

-
1. Commencez par remplacer tous les x par la valeur a dans la fonction f(x).
-
2. Si vous obtenez 0/0 ou
 /
/ alors dérivez le numérateur g(x), puis dérivez le dénominateur h(x) pour obtenir g'(x)/h'(x). Notez que la règle de l'Hospital peut se résumer par la formule suivante :
alors dérivez le numérateur g(x), puis dérivez le dénominateur h(x) pour obtenir g'(x)/h'(x). Notez que la règle de l'Hospital peut se résumer par la formule suivante :
Maintenant appliquez de nouveau le point 1. en remplaçant tous les x par la valeur a dans g'(x)/h'(x). Si vous obtenez un nombre réel, l'infini ou zéro, vous avez votre réponse, le calcul est terminé. Sinon passez au point 3. ...
-
3. ... si vous obtenez de nouveau 0/0 ou
 /
/ alors il faut à nouveau dériver le numérateur et le dénominateur, puis remplacer tous les x par la valeur a, etc.
alors il faut à nouveau dériver le numérateur et le dénominateur, puis remplacer tous les x par la valeur a, etc.
La règle de l'Hôpital peut s'appliquer plusieurs fois de suite, jusqu'à ce que vous obteniez une réponse différente de 0/0 ou de infini/infini.
Exemple :
Nous voulons calculer la limite de la fonction f(x) suivante pour x tendant vers 4.

Rappelons que la règle de l'Hôpital ne peut s'appliquer que dans les cas d'indétermination 0/0 ou infini/infini. Dans notre exemple nous avons la forme indéterminée 0/0, nous appliquons donc l'Hospital.
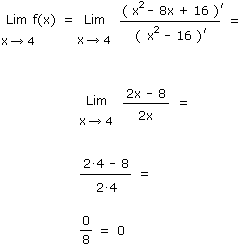
Exercices
1.1 L'Hôpital 3 fois de suite
Soit la fonction f(x) suivante
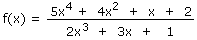
On vous demande de calculer la limite de cette fonction pour x tendant vers l'infini en utilisant la règle de l'Hospital.
1.2 Limite gauche et limite droite
Soit la fonction f(x) suivante

On vous demande de calculer la limite de cette fonction pour x tendant vers 2.
1.3 Lever l'indétermination par factorisation
Soit la fonction f(x) suivante

On vous demande de calculer la limite de cette fonction pour x tendant vers 4.
1.4 Multiplier "haut et bas" par les trinômes conjugués
On vous demande de calculer la limite suivante :

1.5 Calcul de limites et trigonométrie
Calculez la limite suivante :

1.6 Infini moins infini sur infini c'est jamais bon !
Calculez la limite suivante :
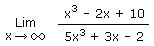
1.7 Sortir un x2 d'une racine comporte un piège
Calculez la limite suivante :

1.8 Le terme du plus haut degré en facteur
Calculez la limite de la fonction f(x) = 9x2 - 2x + 1
pour x tendant vers +infini ainsi que vers -infini.1.9 Factoriser une équation du second degré

1.10 Multiplication par le binôme conjugué
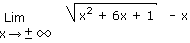
1.11 Le trinôme conjugué encore une fois !

1.12 Limite d'une valeur absolue |x|

1.13 Déterminer une limite graphiquement
Soit la fonction suivante

On vous demande d'utiliser notre machine à calculer graphique en ligne pour visualiser cette fonction dans la fenêtre suivante :
Axe des x : de -5 à +5.
Axe des y : de -100 à +100.
Après cela, répondez aux questions suivantes :
a) Déterminez graphiquement la limite de cette fonction pour x s'approchant de 2 par la gauche. Et la même chose lorsque x s'approche de 2 par la droite.
b) Déterminez mathématiquement (par calcul) les valeurs des limites obtenues en a), c'est-à-dire :

c) La limite pour x -> 2 existe-t-elle ? Si oui, que vaut-elle ? Si non, pourquoi ?
1.14 Limite gauche et limite droite encore une fois !

1.15 D'abord factoriser le polynôme par la Règle d'Horner

1.16 Résolvez comme d'habitude, ça à l'air juste mais c'est faux !

1.17 Utiliser le binôme conjugué puis le trinôme conjugué

1.18 Comment résoudre ça sans l'Hôpital I ?

1.19 Comment résoudre ça sans l'Hôpital II ?
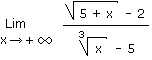
1.20 Infini moins infini comment je fais ?
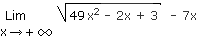
-
-
Commentaires
TOUT SUR LES MATHS AU LYCEE


حل درس